Presentation

The excitation of higher order transverse modes in laser cavities has been studied for a long time, because certain modes have very interesting characteristics. As an example, “vortex” type Laguerre-Gauss modes transport orbital angular momentum; Bessel and Airy beams somehow “resist” diffraction, and are of interest for imaging and optical manipulation of micro- and nanoparticles. We study how structured transverse profiles emerge from the coupling between the spatial distribution of laser gain and the edge conditions imposed by the resonator.

Partial degeneracy and excitation of higher order modes

It has been suggested that it is possible to excite higher order Laguerre-Gauss or Ince-Gauss modes in an optically pumped plano-concave cavity, by optimally positioning the focus point of the pump laser in the plane transverse and properly adjusting its size. We have shown theoretically, on the basis of an overlap integral between the gain and the modal profile, that the excitation of higher order modes with circular or elliptical nodal lines is only possible in the presence of a partial degeneration of the cavity. In this case, we generally obtain a superposition of modes of different order, giving rise to a transverse profile which is not invariant during propagation.

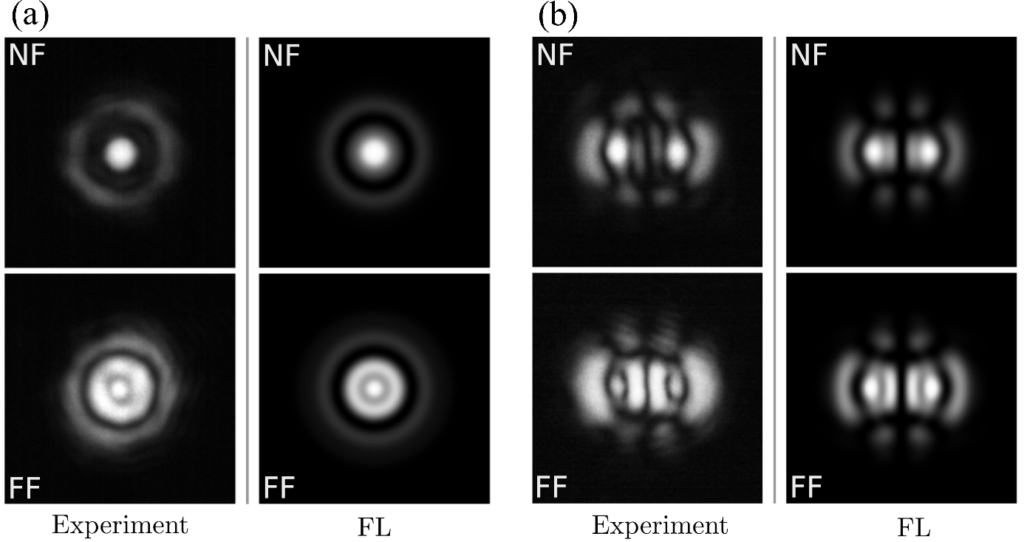
Fig.1 a) Quasi-Laguerre-Gauss mode. (b) Quasi-Ince-Gauss mode. NF: near field. FF: far field. The experiments are compared to Fox-Li (FL) type simulations.

Waves and rays optics: geometric modes

Partial degeneracy effects also manifest themselves in a spectacular manner in so-called “geometric” modes, whose properties can be understood in terms of ray optics.

Fig.2 Experimental observation and Fox-Li simulation of a geometric mode W, obtained by off-axis pumping of a degenerate plano-concave cavity of order 4 (L = Rc/2).

Financial support

Research staff involved

To learn more…

  • Nicolas Barré, Marco Romanelli, Marc Brunel. Role of cavity degeneracy for high-order mode excitation in end-pumped solid-state lasers. Optics Letters, 2014, 39 (4), pp.1022-1025. ⟨10.1364/OL.39.001022⟩. ⟨hal-00947789⟩
  • Nicolas Barré, Marco Romanelli, M Lebental, Marc Brunel. Waves and rays in plano-concave laser cavities, part I. Geometric modes in the paraxial approximation. European Journal of Physics, 2017, 38 (3), pp.034010. ⟨10.1088/1361-6404/aa6461⟩. ⟨hal-01529983⟩
  • A. Pascal, S. Bittner, B. Dietz, A. Trabattoni, C. Ulysse, et al.. Waves and rays in plano-concave laser cavities: II. A semiclassical approach. European Journal of Physics, 2017, 38 (3), pp.034011. ⟨10.1088/1361-6404/aa609d⟩. ⟨hal-01517504⟩

Spatial transverse effects in lasers
Tagged on: