Presentation

Frequency-shifting loops are a simple architecture for generating frequency combs by recirculation of a continuous laser in a loop containing a modulator. We study the behavior of these systems in different configurations (acousto-optic modulator, phase or electro-optic amplitude modulator), for a wide range of applications including in particular microwave photonics.

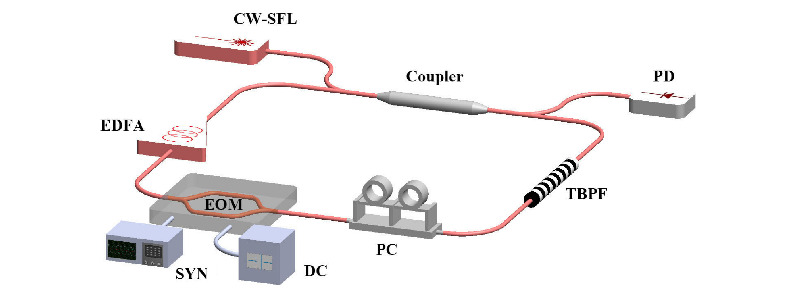
Fig.1 Sketch of a frequency-shifted loop. Here, the modulator is an intensity modulator (EOM).

Acousto-optic (AOM) or single sidedand electro-optic (SSB-EOM) frequency shifting loop

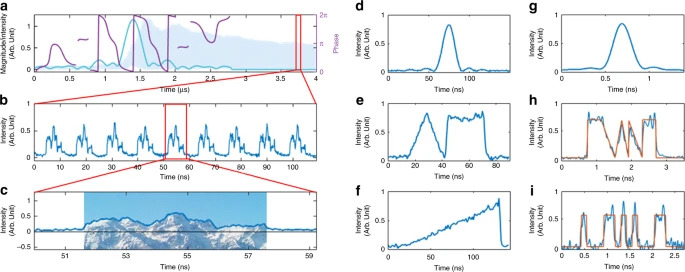
In this case, the loop produces several hundred mutually coherent teeth from the injection laser. The shift frequency (fs), i.e. the spacing of the comb, varies from a few tens of MHz (AOM) to several GHz (SSB-EOM). Unlike a mode-locked laser (where the spectral phase is linear), the spectral phase of the comb is quadratic, and adjustable via the loop parameters (the shift frequency, and the travel time in the loop τc).

When fs and τcare such that their product is a ratio of integers p/q (fractional Talbot condition), the system then produces a pulse train at a repetition rate of qfs. This phenomenon (called temporal Talbot effect) makes it possible to reach repetition rates of the order of several tens of GHz. We also show that the phase noise of the pulse train depends only weakly on the repetition rate.

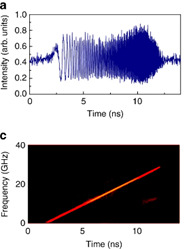
When the system is set in the vicinity of a Talbot condition, the time trace consists of a succession of linear chirps, that is to say optical signals whose frequency varies linearly with time. Heterodyne recombination with the seed laser on a fast photodetector produces broadband RF chirps. The sign and slope of the chirps are easily adjustable, which allows lidar or radar applications to be considered.

Fig.2 Acousto-optic frequency comb. The comb spacing is 80 MHz
Generation of linear chirps in an acousto-optic frequency shifting loop.

Frequency shifting loops containing a phase or an intensity modulator

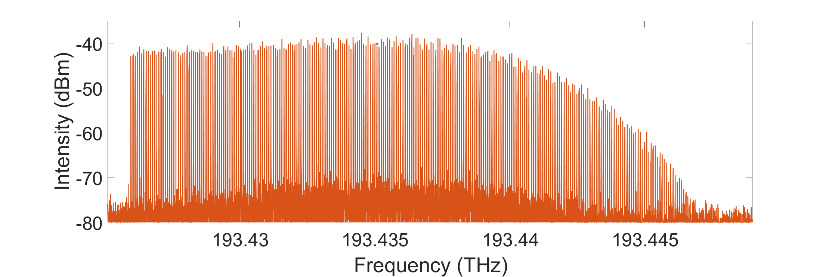
In this case, the spectrum obtained at the output is symmetrical with respect to the frequency of the injection laser and the stabilization of the comb requires control of the length of the loop on the injection frequency. The system then produces several hundred mutually coherent teeth.

When the modulator is an intensity modulator, if the product fsτc is an integer (integer Talbot effect), the system generates doublets with adjustable relative delay. Similarly, a fractional Talbot effect makes it possible to multiply the repetition rate of the output pulses.

When the modulator is a phase modulator, the system also produces pulse doublets in integer Talbot conditions, without offering a fractional effect. On the other hand, near the integer Talbot condition, the system generates non-linear chirps, whose instantaneous frequency reproduces the signal applied to the modulator. This makes it possible to generate optical or RF signals having an arbitrary instantaneous frequency, which again offers prospects for lidar or radar telemetry.

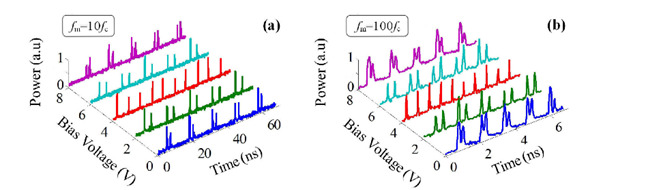
Fig.3 Examples of pulse doublets in a frequency-shifting loop containing an intensity modulator.

Real-time signal processing in frequency shifting loops

When an RF input signal is applied to the laser injecting the loop, the system can be used to generate arbitrary signals, and is akin to a photonic AWG. Indeed, in integer Talbot condition, the output signal reproduces along time the Fourier transform of the input signal. We can therefore program the input signal to obtain very fast arbitrary signals (> 20 GHz bandwidth) at the output.

Symmetrically, the system can be used to calculate the Fourier transform of the input signal. This property is observed in acousto-optic modulator or phase modulator loops. This allows spectral analysis of signals in real time (Fourier transform, fractional Fourier transform). To extend the analysis bandwidth from a few tens of MHz to tens of GHz, a new architecture has been developed, based on a bi-directional frequency-shifting loop. It allows spectral analysis of broadband signals (up to 16 GHz) in real time, and with a 100% interception probability.

Finally, the architecture using a double frequency shifting loop also makes it possible to measure in an analog way, the cross-correlation function of two signals, a fundamental property for example in stellar interferometry, or for the location of RF transmitters.

Fig.4 Example of generation of arbitrary signals in an acousto-optic frequency shifting loop.
Spectral analysis of ambient RF signals (Wi-Fi, cell phone) in an acousto-optic frequency shifting loop.

Financial support

CNRS (Programme Prématuration 2020), Université Grenoble Alpes, ANR (projet COCOA)

Research staff involved

Research engineers, researchers and professors

  • VALLET Marc

    VALLET Marc

    (+33)2 23 23 62 04 Professor Responsable d’équipe

PhD and post-doc

To learn more…

  • H. Guillet de Chatellus, E. Lacot, W. Glastre, O. Jacquin, O. Hugon. Theory of Talbot lasers. Physical Review A : Atomic, molecular, and optical physics [1990-2015], 2013, 88, pp.33828. ⟨10.1103/PHYSREVA.88.033828⟩. ⟨hal-00951890⟩
  • Hugues Guillet de Chatellus, Luis Romero Cortés, José Azaña. Optical real-time Fourier transformation with kilohertz resolutions. Optica, 2016, 3 (1), ⟨10.1364/OPTICA.3.000001⟩. ⟨hal-01693158⟩
  • Côme Schnébelin, Hugues Guillet de Chatellus. Agile photonic fractional Fourier transformation of optical and RF signals. Optica, 2017, 4 (8), ⟨10.1364/OPTICA.4.000907⟩. ⟨hal-01601109⟩
  • Hugues Guillet de Chatellus, Luis Romero Cortés, Côme Schnebelin, Maurizio Burla, José Azaña. Reconfigurable photonic generation of broadband chirped waveforms using a single CW laser and low-frequency electronics. Nature Communications, 2018, 9 (1), ⟨10.1038/s41467-018-04822-4⟩. ⟨hal-01821107⟩
  • Hongzhi Yang, Marc Vallet, Haiyang Zhang, Changming Zhao, Marc Brunel. Pulse doublets generated by a frequency-shifting loop containing an electro-optic amplitude modulator. Optics Express, 2019, 27 (13), pp.18766-18775. ⟨10.1364/OE.27.018766⟩. ⟨hal-02163678⟩
  • Hongzhi Yang, Marc Brunel, Marc Vallet, Haiyang Zhang, Changming Zhao. Analysis of frequency-shifting loops in integer and fractional Talbot conditions: electro-optic versus acousto-optic modulation. Journal of the Optical Society of America B, 2020, 37 (11), pp.3162-3169. ⟨10.1364/josab.389801⟩. ⟨hal-03046194⟩
  • Vincent Billault, Vincent Crozatier, Ghaya Baili, Loic Morvan, Daniel Dolfi, et al.. Phase Noise of Optical Pulse Trains Generated by Talbot Effect in Frequency Shifting Loops. Journal of Lightwave Technology, 2021, 39 (8), pp.2336-2347. ⟨10.1109/JLT.2021.3052041⟩. ⟨hal-04243667⟩
  • Guillaume Bourdarot, Jean-Philippe Berger, Hugues Guillet de Chatellus. Multi-delay photonic correlator for wideband RF signal processing. Optica, 2022, 9 (4), pp.325. ⟨10.1364/OPTICA.442906⟩. ⟨hal-03871320⟩
  • Hugues Guillet de Chatellus. Compact real-time RF spectrum analyzer with 16 GHz instantaneous bandwidth based on photonic frequency-shifting loops. Optics Continuum , 2023, 2 (6), pp.1276-1286. ⟨10.1364/optcon.485987⟩. ⟨hal-04230647⟩

Frequency shifting loops
Tagged on: