⮞ Département DOP ⮞ Thématiques de recherche ⮞ Activité « Optique hyperfréquences et THz » ⮞
Présentation
Les boucles à décalage de fréquence sont une architecture simple pour générer des peignes de fréquences par recirculation d’un laser continu dans une boucle contenant un modulateur. Nous étudions le comportement de ces systèmes dans différentes configurations (modulateur acousto-optique, modulateur de phase ou d’amplitude électro-optique), pour une large gamme d’applications incluant en particulier la photonique micro-onde.
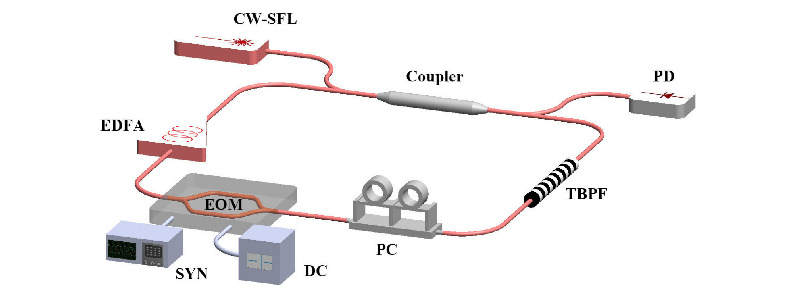
Boucles à modulateur acousto-optique (AOM) ou électro-optique à bande latérale unique (SSB-EOM)
Dans ce cas, la boucle produit plusieurs centaines de dents mutuellement cohérentes à partir du laser d’injection. La fréquence de décalage (fs), c’est-à-dire l’espacement du peigne varie de quelques dizaines de MHz (AOM) à plusieurs GHz (SSB-EOM). Contrairement à un laser à modes bloqués (où la phase spectrale est linéaire), la phase spectrale du peigne est quadratique, et ajustable via les paramètres de la boucle (la fréquence de décalage, et le temps de parcours dans la boucle τc).
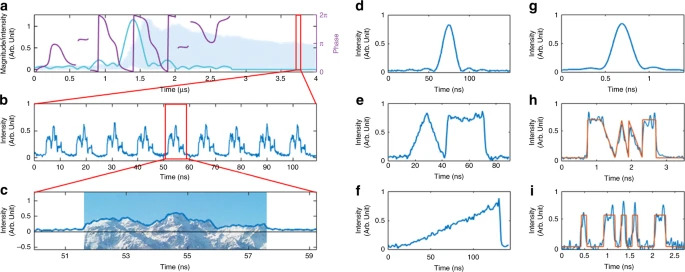
Lorsque fs et τc sont tels que leur produit est un rapport d’entiers p/q (condition de Talbot fractionnaire), le système produit alors un train d’impulsion à un taux de répétition de qfs. Ce phénomène (effet Talbot temporel) permet d’atteindre des cadences de l’ordre de plusieurs dizaines de GHz. On montre par ailleurs que le bruit de phase du train d’impulsions dépend faiblement du taux de répétition.
Lorsque le système est réglé au voisinage d’une condition de Talbot, le signal temporel consiste en une succession de chirps linéaires, c’est-à-dire de signaux optiques dont la fréquence varie linéairement avec le temps. Par recombinaison, on peut facilement produire des chirps RF. Le signe et la pente des chirps sont facilement ajustables, ce qui permet d’envisager des applications lidar ou radar.
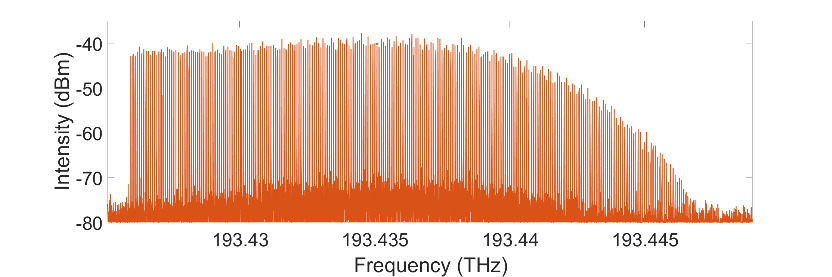
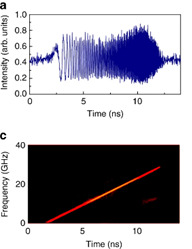
Boucles à modulateur de phase ou d’intensité
Dans ce cas, le spectre obtenu en sortie est symétrique par rapport à la fréquence du laser d’injection et la stabilisation du peigne nécessite un asservissement de la longueur de la boucle sur la fréquence d’injection. Le système produit alors plusieurs centaines de dents mutuellement cohérentes.
Lorsque le modulateur est un modulateur d’intensité, si le produit fs τc est un entier (effet Talbot entier), le système génère en sortie des doublets d’espacement ajustable. De la même manière, un effet Talbot fractionnaire permet de multiplier le taux de répétition des impulsions en sortie.
Lorsque le modulateur est un modulateur de phase, le système produit également des doublets d’impulsions en condition de Talbot entier, sans offrir d’effet fractionnaire. En revanche, au voisinage de la condition de Talbot entier, le système génère des chirps non-linéaires, dont la fréquence instantanée reproduit le signal appliqué au modulateur. Ceci permet de générer des signaux optiques ou RF ayant une fréquence instantanée arbitraire, ce qui offre là encore des perspectives pour la télémétrie lidar ou radar.
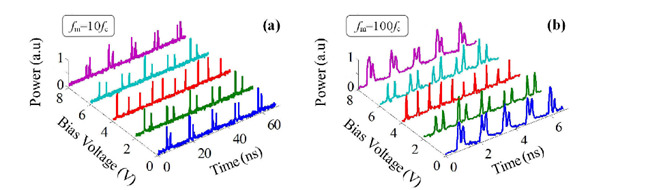
Traitement de signal en temps réel
Lorsqu’un signal d’entrée RF est appliqué sur le laser injectant la boucle, le système peut être utilisé pour générer des signaux arbitraires, et s’apparente à un AWG photonique. En effet, en condition de Talbot entier, le signal de sortie reproduit dans le temps, la transformée de Fourier du signal d’entrée. On peut donc programmer le signal d’entrée pour obtenir en sortie des signaux arbitraires très rapides (20 GHz).
Symétriquement, le système peut être utilisé pour calculer la transformée de Fourier du signal d’entrée. On retrouve cette propriété dans les boucles à modulateur acousto-optique ou à modulateur de phase. Ceci permet de faire de l’analyse spectrale de signaux en temps réel (transformée de Fourier, transformée de Fourier fractionnaire). Pour étendre la bande passante d’analyse de quelques dizaines de MHz à la dizaine de GHz, une nouvelle architecture a été développée et met en oeuvre une double boucle à décalage de fréquence. Elle permet l’analyse spectrale de signaux large bande (jusqu’à 16 GHz) en temps réel, et avec une probabilité d’interception de 100 %.
Enfin, l’architecture utilisant une double boucle permet aussi de mesurer de manière analogique la fonction de corrélation croisée de deux signaux, une propriété fondamentale par exemple en interférométrie stellaire, ou pour la localisation d’émetteurs RF.

Financements
CNRS (Programme Prématuration 2020), Université Grenoble Alpes, ANR (projet COCOA)
Personnels de recherche impliqués
Ingénieurs de recherche, chercheurs et Enseignants-Chercheurs
-

GUILLET DE CHATELLUS Hugues
02 23 23 47 29 Directeur de Recherche
-

BRUNEL Marc
02 23 23 55 73 Professeur des universités
-

VALLET Marc
02 23 23 62 04 Professeur des universités Responsable de département
-

LOAS Goulc’hen
02 23 23 68 81 Ingénieur de recherche
Doctorants et Post-doctorants
-

ALLIOT DE BORGGRAEF Louis
Doctorant (09/2022-11/2024)
Pour en savoir plus
- H. Guillet de Chatellus, E. Lacot, W. Glastre, O. Jacquin, O. Hugon. Theory of Talbot lasers. Physical Review A : Atomic, molecular, and optical physics [1990-2015], 2013, 88, pp.33828. ⟨10.1103/PHYSREVA.88.033828⟩. ⟨hal-00951890⟩
- Hugues Guillet de Chatellus, Luis Romero Cortés, José Azaña. Optical real-time Fourier transformation with kilohertz resolutions. Optica, 2016, 3 (1), ⟨10.1364/OPTICA.3.000001⟩. ⟨hal-01693158⟩
- Côme Schnébelin, Hugues Guillet de Chatellus. Agile photonic fractional Fourier transformation of optical and RF signals. Optica, 2017, 4 (8), ⟨10.1364/OPTICA.4.000907⟩. ⟨hal-01601109⟩
- Hugues Guillet de Chatellus, Luis Romero Cortés, Côme Schnebelin, Maurizio Burla, José Azaña. Reconfigurable photonic generation of broadband chirped waveforms using a single CW laser and low-frequency electronics. Nature Communications, 2018, 9 (1), ⟨10.1038/s41467-018-04822-4⟩. ⟨hal-01821107⟩
- Hongzhi Yang, Marc Vallet, Haiyang Zhang, Changming Zhao, Marc Brunel. Pulse doublets generated by a frequency-shifting loop containing an electro-optic amplitude modulator. Optics Express, 2019, 27 (13), pp.18766-18775. ⟨10.1364/OE.27.018766⟩. ⟨hal-02163678⟩
- Hongzhi Yang, Marc Brunel, Marc Vallet, Haiyang Zhang, Changming Zhao. Analysis of frequency-shifting loops in integer and fractional Talbot conditions: electro-optic versus acousto-optic modulation. Journal of the Optical Society of America B, 2020, 37 (11), pp.3162-3169. ⟨10.1364/josab.389801⟩. ⟨hal-03046194⟩
- V. Billault, V. Crozatier,Vincent Billault, Vincent Crozatier, Ghaya Baili, Loic Morvan, Daniel Dolfi, et al.. Phase Noise of Optical Pulse Trains Generated by Talbot Effect in Frequency Shifting Loops. Journal of Lightwave Technology, 2021, 39 (8), pp.2336-2347. ⟨10.1109/JLT.2021.3052041⟩. ⟨hal-04243667⟩
- Guillaume Bourdarot, Jean-Philippe Berger, Hugues Guillet de Chatellus. Multi-delay photonic correlator for wideband RF signal processing. Optica, 2022, 9 (4), pp.325. ⟨10.1364/OPTICA.442906⟩. ⟨hal-03871320⟩
- Hugues Guillet de Chatellus. Compact real-time RF spectrum analyzer with 16 GHz instantaneous bandwidth based on photonic frequency-shifting loops. Optics Continuum , 2023, 2 (6), pp.1276-1286. ⟨10.1364/optcon.485987⟩. ⟨hal-04230647⟩